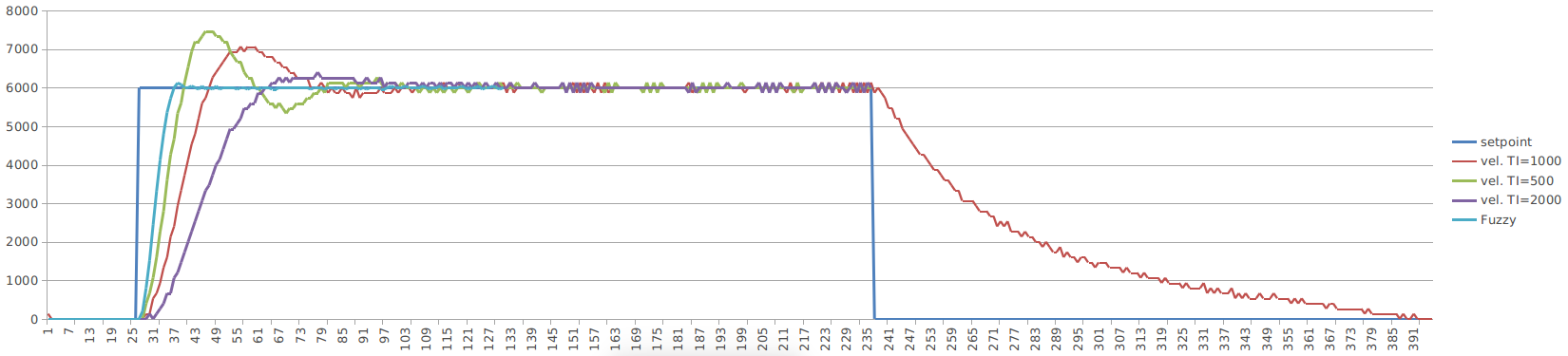
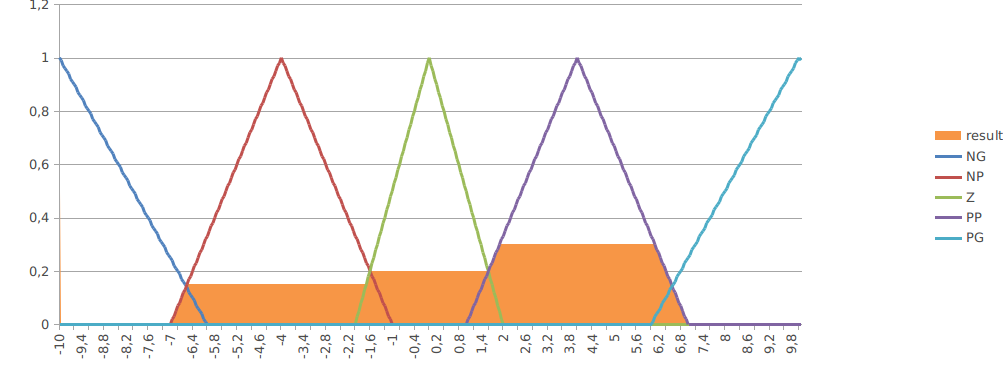
O controlador apresentado abaixo foi testado no controle de velocidade de um motor BLDC de CDROM, no controle de velocidade. Foi comparado com um controlador PID implementado utilizando transformada Z e testado com diferentes parâmetros de integração. O resultado do controle e um caso de ativação de regras podem ser vistos nas figuras anbaixo:
Código:
/* Codigo de um controlador Fuzzy com dois precedentes conectados pelo operador AND. SISTEMAS EMBARCADOS E COMPUTAÇÃO UBÍQUA MESTRADO EM ENGENHARIA DE PRODUÇÃO E SISTEMAS COMPUTACIONAIS – MESC Luciano Bertini */ #include <stdio.h> // Define a estrutura para um conjunto fuzzy triangular, sendo que a ou c podem ser +infinito ou -infinito (INF) struct membership{ float a; float b; float c; }; //Definição de infinito #define INF 1e+6 #define NUM1 5 //Numero de conjuntos na variavel de entrada 1 #define NUM2 5 //Numero de conjuntos na variavel de entrada 2 #define NUM3 5 //Numero de conjuntos na variavel de saida #define MIN(a,b) (((a)<(b))?(a):(b)) #define MAX(a,b) (((a)>(b))?(a):(b)) // Função membership de entrada. r[] é o vetor de pertinencias que será preenchido. // x é o valor sendo fuzificado. z[] é o vetor de conjuntos fuzzy em todo universo de discurso X // n é o tamanho do vetor void test_membership_in(float r[], float x, struct membership z[], int n) { int i; for(i=0;i<n;i++) { if(x<=z[i].a||x>=z[i].c) r[i] = 0.0; else if(x>z[i].a&&x<=z[i].b) r[i] = (x-z[i].a)/(z[i].b-z[i].a); else if(x>z[i].b&&x<z[i].c) r[i] = (z[i].c-x)/(z[i].c-z[i].b); } } // Obtem o valor da membership de saida após a inferência fuzzy. O vetor r[] é entrada e cada valor é // o nível de ativação de cada conjunto fuzzy, obtido na inferencia. Variando-se x em todo universo de discurso, // obtem-se a membership de saida float test_membership_out(float r[],float x, struct membership z[], int n) { float v, ret=0.0; int i; for(i=0;i<n;i++) { if(x<=z[i].a||x>=z[i].c) v = 0.0; else if(x>z[i].a&&x<=z[i].b) v = MIN((x-z[i].a)/(z[i].b-z[i].a),r[i]); // seleciona o minimo entre o nivel de ativação e o triangulo do conjunto fuzzy else if(x>z[i].b&&x<z[i].c) v = MIN((z[i].c-x)/(z[i].c-z[i].b),r[i]); // seleciona o minimo entre o nivel de ativação e o triangulo do conjunto fuzzy ret=MAX(ret,v); // O maximo aqui faz o OU entre dois conjuntos fuzzy i-1 e i } return ret; } main() { int i,j; float de=1.7, e=-1.4; float x,sum1=0.0,sum2=0.0, val, v; float mi1[NUM1],mi2[NUM2],out[NUM3]={0,0,0,0,0}; // Definição dos conjuntos fuzzy struct membership e1[NUM1]={ { -INF, -8.0, -4.0}, { -5.0, -3.0, -1.0}, { -2.0, 0.0, 2.0}, { 1.0, 3.0, 5.0}, { 4.0, 8.0, INF}}; struct membership e2[NUM2]={ { -INF, -8.0, -4.0}, { -5.0, -3.0, -1.0}, { -2.0, 0.0, 2.0}, { 1.0, 3.0, 5.0}, { 4.0, 8.0, INF}}; struct membership s[NUM3]={ {-20.0, -10.0, -6.0}, { -7.0, -4.0, -1.0}, { -2.0, 0.0, 2.0}, { 1.0, 4.0, 7.0}, { 6.0, 10.0, 20.0}}; // Mapa de regras int regras[NUM1][NUM2]={ //horizontal Delta do erro {4,4,3,3,2}, //vertical erro {4,3,3,2,1}, {3,3,2,1,1}, {3,2,1,1,0}, {2,1,1,0,0}}; // Inicialização sum1=0; sum2=0; for(i=0;i<NUM3;i++)out[i]=0; // Fuzificação test_membership_in(mi1,e,e1,NUM1); test_membership_in(mi2,de,e2,NUM2); // Inferencia Fuzzy // O minimo aqui pega o menor dos graus de pertinencias, supondo regras com dois precedentes conectados pelo operador AND // O máximo aqui é util quando um certo conjunto fuzzy de saída já foi ativado antes por outra regra e neste caso deve-se selecionar o maior (OR). for(i=0;i<NUM1;i++) for(j=0;j<NUM2;j++) if(mi1[i]>0&&mi2[j]>0) out[regras[i][j]] = MAX(MIN(mi1[i],mi2[j]), out[regras[i][j]]); // Defuzificação // Calculo do centroide for(x=-10.0;x<=10.01;x+=0.05) { val=test_membership_out(out, x, s, NUM3); sum1+=x*val; sum2+=val; } x=sum1/sum2; printf("saida=%f\n",x); }