Area Evolute and Central Symmetry Set
Given a convex parallel opposite sides polygon (CPOSP) P1P2…P2n we can define:
- Its Great Diagonals: segments di that join Pi and Pi+n (i=1,2,…,n).
- ItsArea Evolute (AE): polygon whose vertices Mi are the midpoints of the Great Diagonals.
- Its Central Symmetry Set (CSS): polygon whose vertices Di+½ are intersections of successive great diagonals.
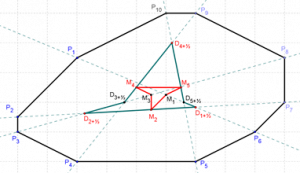
Figure 1. AE (red) and CSS (green) of a CPOSP
Note that:
- The AE reduces to a point if, and only if, the polygon is symmetric with relation to that point (by definition);
- The CSS of a CPOSP reduces to a point if, and only if, the polygon is symmetric with relation to that point.
Cusps of the AE and the CSS
- A cusp of the CSS is a vertex Di+½ such that the orientations of the triangles Di-1+½ Di+½ Di+1+½ and Pi-1PiPi+1 are reversed.
- A cusp of the AE is a vertex Mi such that the orientations of the triangles Mi-1MiMi+1 and Pi-1PiPi+1 are reversed (equivalently: Mi is a cusp if Mi-1 and Mi+1 are on the same side of di).
In this Geogebra applet, the vertices of the AE and of the CSS are marked red whenever they turn into cusps (as you play with the outer polygon).
This is a Java Applet created using GeoGebra from www.geogebra.org – it looks like you don’t have Java installed, please go to www.java.com
For non-degenerate positions (see [1] for proofs):
- The number of cusps in the CSS is odd and at least 3;
- The number of cusps in the AE is odd and at least 3;
- A vertex of the AE is a cusp if, and only if, it belongs to the CSS.
Alternate CSS cusp definition
If we define λi+½ (i=1,2,…,2n) by the equations
Di+½ = Pi + λi+½·(Pi+n – Pi) = Pi+1 + λi+½·(Pi+1+n – Pi+1)
then we have
Di+½ – Di-1+½ = (λi+½ – λi-1+½)(Pi+n – Pi)
Now, in a CPOSP, the great diagonals Pi+n – Pi “turn” in the same orientation as the polygon itself. Therefore the triangles Di-1+½ Di+½ Di+1+½ and Pi-1PiPi+1 have opposite orientations if and only if
(λi+½ – λi-1+½)(λi+1+½ – λi+½)<0
In short
Di+½ is a cusp of the CSS if, and only if, λi+½ is a local extremum of the cyclic sequence {λi+½}
References
[1] M. Craizer, R. Teixeira and M. Horta, “Parallel Opposite Side Polygons”, preprint.
