Fix a point X in the interior of a convex region R. Each line which goes through X divides R in two regions of areas A1 and A2. Of all such lines, pick the one that determines the smallest possible area A1 (and, consequently, the largest A2). This minimum value of A1 is called the Area Distance from X to the border of R. Since X is arbitrary, this actually defines the Area Distance Function (which assigns a “minimum area” to each point in R).
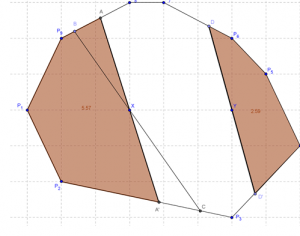
The area determined by BC is bigger than the area determined by AA’ (which is actually minimum for that X). The Area Distance is 5.57 at X, and 2.59 at Y.
The Area Distance starts at 0 at the border of the region and increases as you move “inwards”. It is not hard to see that the minimizing chord at X must have X as its midpoint (see figure above for a polygonal illustration). For more interesting properties of the Area Distance (including a Fast Marching algorithm to calculate it when dealing with polygons), see [2] and the references therein.
Now, let the region R be the interior of a CPOS polygon P. Given a real number λ (less than half the area of R), if you can find some chord which has X as a midpoint and determines an area of λ on one of its sides, we say that X belongs to the λ –Area Parallel (λ would be a candidate value for the area distance at X, but we do not require anymore that the determined area be a global minimum). So the Area Parallels are a slight modification of the level curves of the Area Distance.
You can divide your polygonal region in a mesh of parallelograms using the midpoints of all sides and diagonals, as in the picture below. One can show that, inside each parallelogram, the Area Distance Function is bilinear, so the Level Curves will be the union of many hyperbola arcs, one inside each parallelogram. Let us focus only on the intersections of the level curves with the sides of the parallelograms, and instead of drawing the actual hyperbolas, let us just join such points by line segments, generating an Area Parallel Polygon.
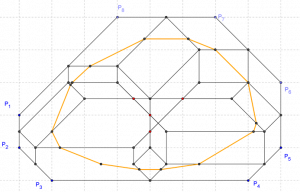 All black dots on the orange polygon have the same Area Distance (2 grid squares), and belong to the same 2-Area Parallel.
All black dots on the orange polygon have the same Area Distance (2 grid squares), and belong to the same 2-Area Parallel.
This next applet allows you to choose your Area Level, and draws the Area Parallel Polygon which corresponds to that Level.
This is a Java Applet created using GeoGebra from www.geogebra.org – it looks like you don’t have Java installed, please go to www.java.com
Things to note (proofs in [1]):
· In a CPOSP, each segment of the Area Parallel Polygon is either parallel to some diagonal, or passes through the midpoint of some side of the original polygon.
· A vertex of the Area Parallel Polygon is a cusp if and only if it belongs to the Area Evolute (in the Applet, the maximum λ allowed is exactly the point where the first cusp would be formed, right at the AE).
[1] M. Craizer, R. Teixeira and M. Horta, “Parallel Opposite Sides Polygons”, preprint.
[2] M. Craizer, R. Teixeira and M. Horta, “Area Distances of Convex Plane Curves and Improper Affine Spheres”, SIAM Journal on Imaging Sciences, v. 1, p. 209, 2008.