Cusps and the Affine Evolute

Definitions

Given a CEA polygon P₁P₂…P_N, we define:

·        The affine normal at P_i is the vector n_i=P_i-1+P_i+1-2P_i (which is “twice the median” of P_i-1P_iP_i+1);

·        The λ-parallel polygon has vertices P_i(λ)=P_i+λ.n_i. Its sides are indeed parallel to the sides of the original CEA polygon. As λ varies, the λ-parallel polygons perform an affine evolution of the original CEA polygon.

·        When the λ-triangle P_i-1P_iP_i+1 has a different orientation than the original P_i-1P_iP_i+1, we say that P_i(λ) is a cusp of the λ-parallel polygon.

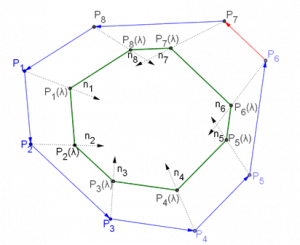
Affine normals and the 0.6-parallel polygon. No cusps yet…

·        The affine evolute is a polygonal curve with vertices q_i= P_i(1/μ_i)=P_i+n_i/μ_i. More precisely, if μ_iμ_i+1>0, the segment q_iq_i+1 is part of the evolute; but, if μ_iμ_i+1<0, the affine evolute includes the portion of the line q_iq_i+1outside the segment q_iq_i+1.

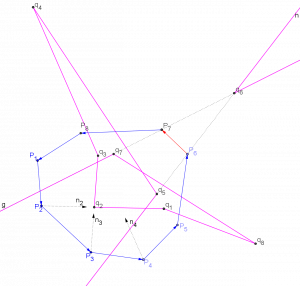
Affine evolute. Since μ₆<0, “sides” q₅q₆ and q₆q₇ go through “improper points at infinity”.

Cusps and the Affine Evolute

In the Geogebra Applet below, you can construct your own CEA octagon (moving P₁-P₆) and play with the λ-parallel polygons (dragging λ – if your mouse hand is tired, just press the “play” button on the lower left corner and we will move λ around for you J). Whenever a vertex turns into a cusp, we mark it red.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Things to note:

·        In a CEAP, P_i(1/μ_i)= P_i+1(1/μ_i), so the vertices q_i correspond to “shocks” of the Affine Evolution.

·        In fact, the affine evolute turns out to be exactly the set of all cusps!

·        The affine evolute reduces to a single point if, and only if, the original polygon is regular (modulo an affine transformation).

·        When a curvature associated to an edge of the original polygon is negative, that edge becomes red. For example, in the original position, P₆P₇ is red because length(P₅P₈) > 3 .length(P₆P₇) and thus μ₆<0. Note how P₆(λ) determines two disconnected branches of the Affine Evolute (and so does P₇(λ)).

Reference

[2] M. Craizer, R. Teixeira and M. Horta, “Affine properties of convex equal-area polygons”; Discrete & Computational Geometry, October 2012, Volume 48, Issue 3, pp 580-595.